'원대칭'을 정의해보자
원대칭은 '원윗점대칭'과 '접선대칭'으로 구분하겠다.
1)원윗점대칭
원 위를 움직이는 모든 점에 대해 원 밖의 특정한 점을 대칭시키고 자취를 표시해 원윗점대칭을 구현한다.

2)접선대칭
원 위의 모든 접선에 대해 원 밖의 특정한 점을 대칭시키고 자취를 표시해 접선대칭을 구현한다.

탐구에 앞서 몇 가지 설명을 할 부분이 있다. 원은 회전을 시켜도 같은 모양이 유지되기에 대칭시키고자 하는 점은 x축 위의 점(a,0), 대칭시키고자 하는 직선은 y축과 평행한 x=a, 대칭시키고자 하는 원은 중심이 x축 위에 있는 (x-a)^2+y^2=r^2으로 봐도 상관 없다. 결국에 각도를 돌려 보면 같은 모양이 되기 때문이다. 이때 접선대칭과 원윗점대칭의 기준이 되는 원은 중심이 (0,0)이고, 반지름이 R인 원(이하 C1)이라 하자. 대칭했을 때 나오는 모양은 R과 a의 비율에 따라 바뀐다는 프로그램을 통해 안 결과에 의해, a/R=k라 하자.(R>0, r>0)
지오지브라 프로그램을 통해 대칭을 확인했다. 점, 직선, 원에 대해 원윗점대칭과 접선대칭을 보며 일정한 규칙을 알아냈다. 지오지브라를 통해 대칭을 한 방법은 점, 직선, 원에 대해 기준 원 위의 한 점 혹은 접선에 대해 대칭을 하고, 그 자취를 표시하는 방법을 이용해 표현했다.
https://www.geogebra.org/classic/wcgepgv9
지오지브라 클래식 - GeoGebra
www.geogebra.org
지오지브라로 관찰한 결과(k와 -k일 때 나오는 모양은 y축에 대칭), 원윗점대칭에서는 점(pp)을 원윗점대칭 할 땐 지름이 4R, 중심이 (-a,0)인 원을 그린다.(이 원은 접선대칭에서의 같은 k 일 때 나오는 모양에 내접한다.)

직선 (lp)을 원윗점대칭 할 때는 –a-2R<=x<=-a+2R(구간)이 나온다.
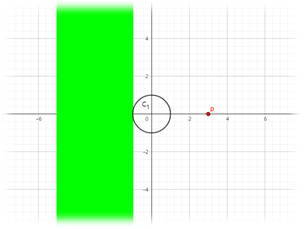
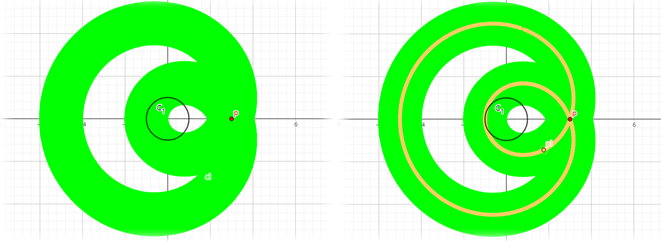
원(cp)을 원윗점대칭 할 땐 반지름이 2R+r, 중심이 (-a,0)인 원에서 반지름이 |2R-r|, 중심이 (-a,0)인 원을 뺀 도넛 모양이 나온다.
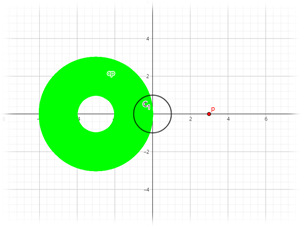
접선대칭에서는 점(pl)의 경우에는 k에 따라 모양이 다른데, |k|=0 일 땐 원이 나온다.
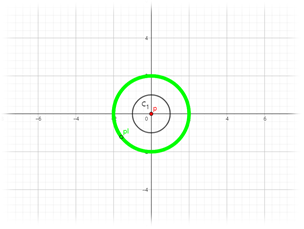
0<|k|<1 일 땐 원에서 절댓값이 커질수록 점점 찌그러진다.
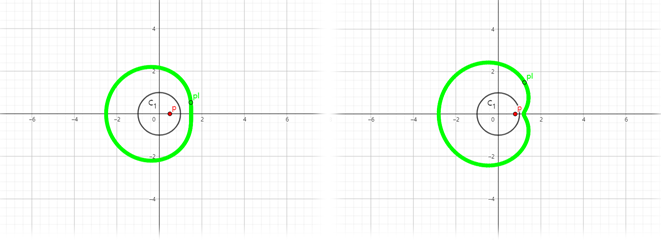
|k|=1 일 땐 에피사이클로이드(카디오이드 곡선) 가 나온다.
(다음 포스팅에서 증명하도록 하겠다.)
|k|가 매우 커지면 원(고리가 원형이 돼 겹침)이 된다.
직선(ll)의 접선대칭하는 경우에도 k에 따라 모양이 다른데,
|k|<=1 일 땐 모든 순서쌍이 나온다.

1<|k| 일 땐 k일 때의 점들이 그린 고리 안쪽을 제외한 모든 순서쌍이 나온다.
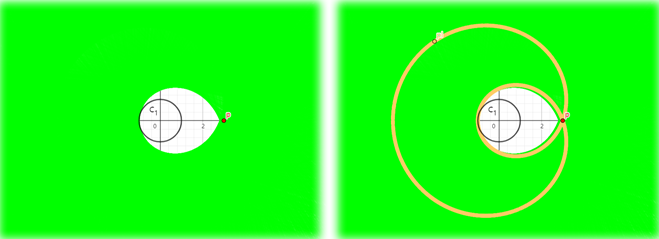
원(cl)을 접선대칭할 땐 반지름이 r인 원이 같은 k일 때 점의 원윗점 대칭에서 나오는 경로를 따라 움직이는 자취가 나온다.
점을 접선 대칭 할 때 나오는 곡선이 마치 에피사이클로이드 모양과 비슷하여 지오지브라를 통해 비교를 해보니 일치했다. 그렇기에 이를 접선의 방정식을 활용해 수학적으로 이 곡선이 에피사이클로이드임을 증명하였다. 이 내용은 다음 포스팅에서 소개하겠다.
다음 포스팅->
https://nomadsjh.tistory.com/4
원대칭으로 만든 카디오이드 곡선에 관한 증명
우리가 정한 원대칭이라는 정의와 같은 곡선의 식은 https://www.geogebra.org/classic/vjq8fbkk 지오지브라 클래식 - GeoGebra www.geogebra.org
nomadsjh.tistory.com
'수학' 카테고리의 다른 글
| [수학] 행렬의 곱셈 (1) | 2023.10.11 |
|---|---|
| [수학] 행렬의 덧셈, 뺄셈, 실수배 (2) | 2023.10.05 |
| [수학] 행렬의 개념 (0) | 2023.10.05 |
| [수학] 미적분학의 기본정리 1 유도 (0) | 2023.08.18 |
| [수학탐구] 원대칭으로 만든 카디오이드 곡선 증명 (0) | 2022.10.12 |





