[수학] 역삼각함수에 대하여(1) - 그래프의 개형
우리는 기본적인 삼각함수인 sin, cos, tan, sec, csc, cot에 대해 들어본 바 있습니다.
또한 우리는 역함수의 개념에 대해서도 접해보았죠.
이번 포스팅에서는 삼각함수의 역함수인 역삼각함수에 대해 살펴볼 것이고 특히 그래프의 모양에 대해 알아볼 것입니다.
| 역삼각함수의 그래프 |
역함수의 그래프는 y=x 대칭을 이용하여 그릴 수 있습니다.
이때, 역함수는 일대일대응 구간에 대해 성립하기 때문에 삼각함수의 모든 구간에 대해 역함수를 정의할 수는 없습니다.
따라서 삼각함수의 일대일대응인 구간에 대해서만 역함수를 만들 수 있는 것이죠.
(일대일대응이란 x 한 개에 y 한 개가 대응하고 y한 개에 x 한 개가 대응하면서 공역과 치역이 같은 함수를 말합니다.)
먼저, 사인함수(sin)의 그래프를 예시로 들어 이해해보겠습니다.
- y=sin(x) 역삼각함수
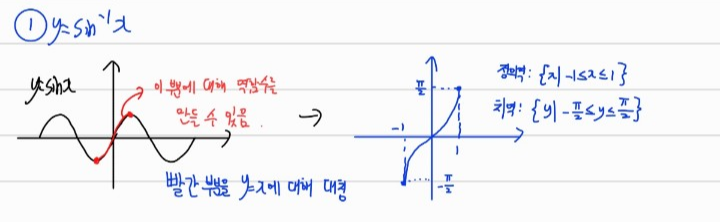
그림 중 왼쪽의 빨간 부분은 일대일대응입니다.
정의역은 -pi/2 <= x <= pi/2이고 치역은 -1 <= x <= 1인 구간을 말하는 것입니다.
이 구간을 y=x 대칭하면 y=sin^-1(x) 그래프를 그릴 수 있습니다.
y=x 대칭되었기 때문에 정의역과 치역도 서로 바뀌게 되고 그래프 개형은 오른쪽 위와 같아집니다.
이러한 과정을 다른 삼각함수에도 적용하여 역함수를 도출할 수 있습니다.
- y=cos(x) 역삼각함수

y=cos(x)의 일대일대응 구간만을 그린 것이고 그것을 y=x 대칭하여 오른쪽 그래프를 나타내었습니다.
또한 역삼각함수의 정의역과 치역 역시 제시해 놓았으니 참고하시기 바랍니다.
- y=tan(x) 역삼각함수

- y=csc(x) 역삼각함수

csc, cot, sec 함수는 사실 원함수의 개형도 어색합니다. 각각이 sin, tan, cos의 역수라는 사실을 이용하여 그래프 개형을 왼쪽 위와 같이 유추할 수 있습니다.
sin(0)=sin(-pi)=sin(pi)=0이기 때문에 csc(x), 즉 1/sin(x) 의 정의역으로는 0, -pi, pi가 포함될 수 없습니다.
그래서 점근선이 됩니다. 그리고 x값이 변함에 따라 sin(x)값이 어떻게 변하는지를 통해 csc(x) 그래프의 개형을 그릴 수 있는 것이죠. 아래 그래프들에도 동일한 원리가 적용됩니다.
- y=cot(x) 역삼각함수

- y=sec(x) 역삼각함수

이렇게 역삼각함수의 그래프 개형에 대해 알아보았습니다.
다음에는 역삼각함수의 기본 성질들과 증명, 도함수에 대해 다뤄보겠습니다. 감사합니다!