[수학] 평균값 정리와 증명

이전 글>> 롤의 정리와 증명 : https://nomadsjh.tistory.com/61

 

평균값 정리란?

평균값 정리란 닫힌 구간 [a, b]에서 연속이고 열린 구간(a, b)에서 미분가능한 함수 f(x)는 다음을 만족시키는 c가 (a, b)에 적어도 하나 존재한다는 정리입니다. $$\frac{f(b)-f(a)}{b-a}={f}'(c)$$

 

말로 풀어서 설명하면 특정 구간에서 정의된 미분 가능한 함수는 구간의 평균변화율과 같은 순간 변화율을 가지는 점을 반드시 가진다는 의미입니다.

 

이전 글에서 증명한 롤의 정리를 이용하여 평균값 정리를 유도할 수 있고 평균값 정리는 롤의 정리를 일반화한 것이라고 할 수 있습니다. 따라서 평균값 정리의 특수한 경우가 롤의 정리인 것이죠. f(a) = f(b)를 대입하면 롤의 정리와 같다는 것을 알 수 있습니다.

 

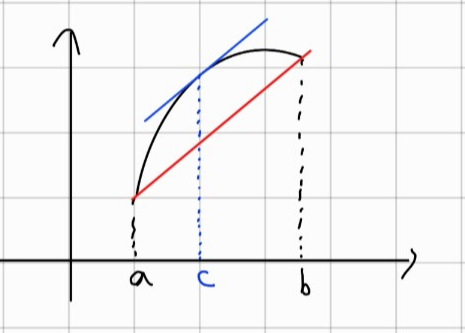
증명

h(x) = f(x) - g(x)라고 할 때 함수 h(x)는 [a, b]에서 연속, (a,b)에서 미분가능합니다.

h(a) = f(a) - g(a) = 0, h(b) = f(b) - g(b) = 0

따라서 h(a) = h(b)이므로 롤의 정리에 의해 h '(c) = 0인 c가 열린 구간(a, b)에 존재합니다.

h '(x) = f '(x) - g '(x)이므로

h '(c) = 0 ↔ f '(c) = g '(c) ( = g(x)는 일차함수이므로 함수의 기울기값) ↔ $$\frac{f(b)-f(a)}{b-a}={f}'(c)$$

 

이렇게 롤의 정리에 이어서 평균값 정리까지 살펴보았습니다. 감사합니다.